前回の投稿に続きまして、リレー講習後半の様子をレポートいたします。

４日目

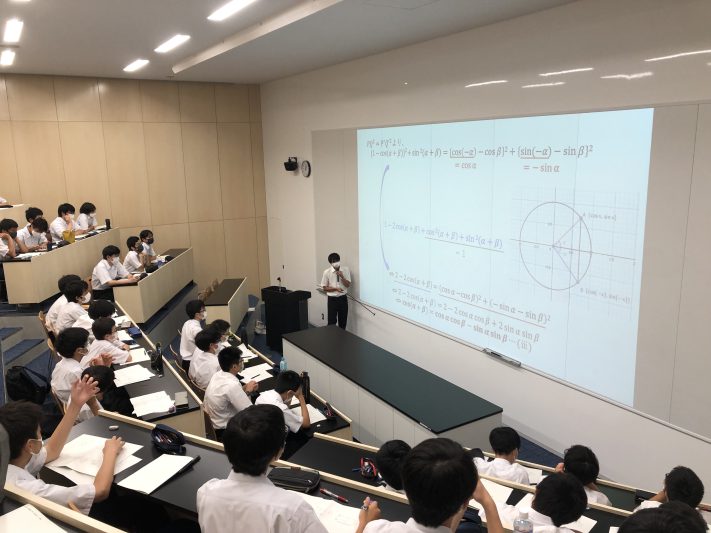
　リレー講習の四日目では、オイラーの公式を理解するための準備として三角関数について扱いました。
　講座の前半は、単位円をもとにした三角関数の定義から始まり、鋭角の場合の図形的意味、相互関係、角度変換、グラフについて解説しました。３種類の正弦曲線を合成しただけで、グラフが複雑化することに驚いている生徒が多いことが印象的でした。
　後半では、三角関数の加法定理の証明、弧度法について扱いました。前向きに聞いてくれる生徒が多く、今まで慣れ親しんだ度数法に代わる弧度法についても、すぐに理解してくれました。
　授業の最後には、y=sinxを原点周りで近似した多項式の例示をしていきました。グラフを示すことで、y=sinxと近似した多項式の関係を見つけることができたようです。今日の講習が、明日以降の理解の助けになると嬉しいです。（下田・天野）

５日目

　5日目は前半で，e^x, sin x, cos xの導関数を目標に微分についての説明を，後半で，それらの関数をべき級数展開することを目標にテイラー展開の説明をしました。
　数学Ⅲから大学初年度の内容なので，説明では数学としての正確さは大切にしつつも全体のイメージがつかめるように心掛けました。まず，前日までに示された主要な関数の導関数を，x=aにおける微分係数の定義から始めて正確に導き，定義式の形より接線が曲線を近似する最も簡単なグラフであることをみていきました。次に，よりよい近似のために1次の接線から次数を上げ，n次の剰余項を評価してテイラーの定理を，剰余項が0に収束する場合にテイラー展開ができることを導きました。その上で，e^x, sinx, cosxのべき級数展開を求め，アプリを用いて多項式のグラフが収束してく様子をみて講習を終わりました。
　難しい内容でありながら，80分間集中が途切れず聞いてくれました。数学を学ぶ者が大切にする「気持ち」が少しでも伝わっていれば嬉しいです。（長澤・平山）

６日目

　リレー講習の最終日の目標は、5日目までで準備した事を用いてオイラーの等式（e^{πi}+1=0）を理解することです。まずe^x、sinx、cosxの冪級数展開を用いてオイラーの公式を簡単に証明しました。（数学的に細かい話は講義録に委ねる形で、形式的に証明を理解することに徹しました。）次に複素数の複素数乗を定義し、√iやi^iなどを実際に手を動かして計算しました。特に、0でない複素数wに対して、w=e^zとなるzが無限に存在することにも触れ、多価関数という立場をとれば、i^iはいろいろな値をとってしまうということも説明しました。最後に三角関数の加法定理を指数法則を用いて証明し（もちろん加法定理はsinの導関数を導く際に用いているので循環論法ではあるが）、実際に三角関数で表される現象の解析にはオイラーの公式が強力な武器になりそうだということを実感しました。
　最終日なので難しそうな表情を浮かべつつも、ノートを一生懸命にとっている生徒の姿が印象的でした。6日間、お疲れさまでした！（柴山）

６日目の資料

生徒の感想

難しかったものの、数学の奥深さを知ることができて良かった。もっといろいろ調べてみたい。（中２）

私はこの講習を受けてみて、多くのことを知った。これまで「何かよくわからないやつ」ぐらいの認識だったsinやcos、名前ぐらいしか知らなかったi、そもそも存在を知らなかった無限級数などだ。講習が終わっても正直完全に理解したとはとても言い難い状態なのだが、前半3日間の内容も含めて多くの事を学んだはずだ。特に印象に残っているのは、やはりオイラーの等式だ。最初にこの式を見たときは、その式の意味も目的も何も分からなかった。それどころかそれぞれの文字の意味さえよく分かっていなかった。しかし、この前半後半を合わせて6日間の講習を経て、何とか薄い表面の部分ぐらいは理解できたのではないかと思う。この体験は今すぐには役に立たないかもしれないけれど、高校の授業なので、この範囲を学ぶときは存分にこれを活かしていきたい。（中３）

理解できないところもかなりあったが、ある程度土台ができてからの6日目の授業は分かるところも多かった。自分は中３なので2学期から三角関数をやると思うが、リレー講習を通してその内容を確認できたのはよかった。（中３）

自分たちの学んでいた数学の範囲をものすごく進化させた分野を取り扱った6日間。恐らくこの先自分が学んでいくであろう「三角関数」や「指数・対数」、「虚数（複素数）」、「微分」に関して周りより一歩先に学べたのは嬉しかった一方、数学における様々な矛盾や議論を見て数学の世界がいかに広いか実感できました。でも正直言うと全ての分野がめちゃくちゃ難しかったです。（中３）

僕は今回リレー講習を受けて、今まで単語だけを何となく知っていた三角関数のcosやsin、微分などを断片的ではあるが理解することができた。また、多項式関数のグラフが次数を上げていくにつれてy=cosxに似た曲線になっていくのが面白いと思った。途中の加法定理などで頭が追いつかなくなったり難しい部分はたくさんあったが、「世界一美しい公式」と言われているオイラーの等式がどのような事を表しているのか理解することができた。これから授業で三角関数や複素数などを学んでいくと思うが、今回の講習で学んだ関係性などを頭に入れた上で学んでいきたい。（中３）

前半に比べて後半も三角関数からの微積分となかなかボリューミーだった。三角関数やe^xを冪級数で表すというのには数学の奥深さを感じた。i^iが無限に存在するというのには驚いた。この講習で今まで習ってきた色々な単元の繋がりを感じられてよかったと思う。（高１）

オイラーの公式について、もともと名前だけは知っていたが、その証明方法やどのようなときに活用できるかなど詳しいことについてはあまり理解していなかったのでこの講習を受けることにした。最初は微積分や三角関数を既に知っていたこともあり、理解しやすい内容だったが、2日目から次第にテイラー展開など解説を聞いても理解するのが難しい内容へ進み、一部分からない点もあった。しかし、先生方の分かりやすい解説によりオイラーの公式を何とか理解できた。難しい点も多かったが、今回の講習は非常に貴重な体験となった。（高１）

三角関数と指数関数が組み合わさっていて難しかったですが、なんとか理解できたような気がします。sinとcosで無限級数を簡単な式にしてしまうところに感動しました。6日間ありがとうございました。（高２）