「化学と数学」の特別講座も第３回を迎えました。
分子の対称性を群を用いて記述することにより、分子軌道を求めることができます。
今回は、アンモニアを例に分子の対称性を考えました。
また、化学編では「分子軌道がわかれば、化学のすべてがわかる」理由を簡単に紹介しました。

これまで、群の定義を定着させるべく、種々の数の集合と四則演算で、あるいは、操作の集合と操作の合成で、それぞれのペアが群をなすか否かを、繰り返しチェックし、どうやら、巡回群、クラインの４元群、３次対称群といった諸例についても理解が進んできました。これ、全ては分子の対称性を記述するための準備でありました。
まずはH2Oの対称性を記述することからスタート。鏡映を考慮することにより、これは既習のクラインの４元群で記述されることが分かりました。
つぎにNH3の対称性を考えました。これは、若干の考察により、３次対称群で記述されることが分かり、参加者一同、「なるほど」とうなずいていました。
CH4の対称性を表す群の決定を宿題とし、最後に群の共役類について紹介しました。
これは、分子の対称性を群で記述した後、その群の指標表を作成することができれば、
なんと、分子軌道（MO）が判明し、MOが分かれば「化学反応の全容が分かる」という福音へいざなうためです。
通常は、MOの判明には極座標と微積分を利用するそうですが、群の利用による道もあるそうです。
ただし、化学者の多くはその道は歩まないとのこと。さて、俄然、楽しくなってきたこの講座ではありますが、そもそも、
MOとはどういったものなのでしょうか？というところで、バトンは平田先生に渡されたのでした。








さて、ここからは川崎先生に代わり、平田がレポートします。
分子軌道がわかれば、化学反応のすべてが分かります。通信販売のうたい文句みたいに聞こえますが、実際すべてわかってしまいます。さて、それはどういうことなのか、説明しましょう。
分子軌道の話をする前に、原子軌道の話をしなければなりません。原子は、中心に正電荷をもった原子核と、それをとりまく負電荷をもった電子から構成されます。この電子の状態をあらわしたものが原子軌道です。電子は粒子としての性質と波動としての性質をあわせもつので、その状態（位置や速度）を従来の力学で表現することはできません。その代わりに、電子の状態は確率を用いて表現されます。電子が存在しうる領域の差を、色の濃淡で表したものが電子雲という考え方です。その後、シュレディンガーは粒子である電子のふるまいを波動方程式で表現しました（シュレディンガーの波動方程式）。水素原子についてシュレディンガー方程式を解き、原子エネルギーに対応した許される関数（1s, 2s, 2p･･･）が原子軌道です。電子を２個以上もつ原子においては、エネルギーの低い軌道から電子をつめていくと、様々な原子の電子のふるまいを近似的に解くことができます。
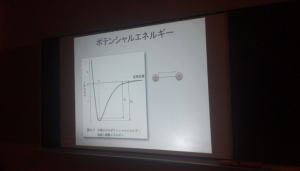
次に、分子軌道とは、構成する原子の原子軌道が結合してできる軌道です。原子同士が結合すれば、新しくできたより安定な軌道に電子が配置されます。この分子の波動方程式を解くことによって、分子のもつエネルギーを求めることができます。例えば、水素分子では、原子核間距離が無限大のところからだんだん小さくなるとき、核と電子の引力がはたらいてエネルギーが小さくなり、最小値を迎えます。この最小値、つまり平衡核間距離よりも小さくなると、核間斥力が増大してエネルギーが大きくなります。また、水分子では、対称性を考慮しても、O−H結合の距離の他にH−O−Hの結合角というファクターによって分子のエネルギーが決まります。さらに複雑な分子になると、さらに多くのファクターによって分子のエネルギーが決まりますが、それらをすべて含めて、最小値となる点が分子の最安定構造となります。
化学反応は分子を構成する原子の結合の仕方が変化する、つまり結合距離や結合角が変化していきます。それに伴って、分子のエネルギーも変化します。化学反応の中でもキーとなる結合距離や結合角などのファクターを平面座標軸にとり、縦軸にエネルギーをとったものをポテンシャルエネルギー曲面（PES）といいます。化学反応では、反応系の最小値から、PESの”轍”を通り、生成系の最小値にエネルギーと構造が変化していきます。
現代化学においては、このような計算をコンピュータで行うことによって、分子の構造や反応をシミュレーションする分野が確立されています（「計算化学」という分野です）。分子軌道がわかれば、実験をせずに、このような方法で物質の性質や反応性を知ることができます。ただし、現在の数学的技術やコンピュータ技術では、分子軌道を近似的に解くことしかできません。今後、数学やコンピュータがさらに発展すれば、近似せずに正確に解くことによって、化学の世界がさらに発展することが考えられます。化学と数学の架け橋になろうと思っている皆さんなら、貢献してくれると思います。今後の活躍に期待します。